从零开始深度学习

深度学习

CH3 安装环境

  • 我有 NVIDIA 的独显 因此可以安装 CUDA 使用 GPU 来跑深度学习 去官网下载新版即可 注意如果不想装在系统盘 需要自定义安装

  • 安装 Anaconda 或是 miniconda 我选择 Anaconda 可以参考这个：https://www.jianshu.com/p/eaee1fadc1e9

    注意如果安装了 python 版本为 3.12 的 anaconda 在安装 d2l 时会报错 我选择使用conda create --name d2l python=3.9 -y指令创建一个 3.9 版本 python 的环境来进行学习

  • 安装 Pytorch 去官网下：https://pytorch.org/get-started/locally/

  • 安装 jupyter 和 d2l 使用 pip 即可

  • 下载提供的笔记本 本地运行 jupyter 进入某一个章节进行测试

（可选）使用 VS Code+Jupyter 来快速浏览笔记本

每次都使用 anaconda 的 shell 运行 jupyter 非常不方便 可以直接下载 vscode 的 jupyter 扩展 然后选择内核为对应的 python（比如我用 3.9） 然后就可以在 vscode 里浏览笔记啦

CH4 数据处理

  • torch 提供和 numpy 类似的一系列数组操作 不过在这里数组其实是张量（tensor）

  • os 库可以对文件进行操作 panda 库可以对 csv 文件进行读取插值等操作

  • 使用 fillna 函数对数据进行插值 get_dummies 函数可以把 NaN 和其他值分开为两列

CH8 线性回归+基础优化算法

线性回归

  • 线性模型即输出=n 维输入的加权线性组合 可以看做是单层神经网络 即只有输入层和输出层的神经网络

  • 损失函数是用于衡量实际值和预测值差距的 在回归问题中最常用的损失函数是平方损失 即方差

  • 求解过程即最小化损失函数的过程 实际上就是最小二乘法

  • 因为损失是凸函数 所以线性回归是具有显式解的

  • 基本过程就是 读取数据 定义模型 定义损失 定义算法 初始化参数 开始训练

基础优化算法

  • 梯度下降法：沿反梯度方向更新参数求解
  • 小批量随机梯度下降：采用某几个训练集的样本来计算梯度 近似损失 减少开销 这是深度学习默认的求解算法 重要参数是批量大小和学习率

CH9 Softmax 回归+损失函数+图片分类数据集

Softmax 回归

  • Softmax 回归并不是回归 而是分类算法 输出有多个 分别是每个类的置信度

  • 对于类别进行一位编码 即哪个类别就置哪一位为 1 使用 MSE 损失训练 取置信度最大的类别为预测值 期望预测类别的置信度要远大于其他类别 得到更加置信的结果

  • 我们希望输出符合概率的形式 即非负且和为 1 因此我们把输出向量做 softmax 函数处理 即指数函数归一化 这样每个输出就可以作为预测概率

  • 我们常使用交叉熵来衡量概率向量的差距 因此损失函数采用预测向量和真实向量的交叉熵 而其梯度刚好就是真实概率和预测概率的差（可推导）

  • 实现流程

    首先说明这个模型是怎么样的：输入一个特征向量 x（比如输入一张图片就是展开的向量）对这个向量 x 进行加权线性组合以及附加偏移可以产生一个向量 y 其维度和分类数一致 最后对 y 进行 softmax 处理 得到同维度的向量 P 这个 P 就是置信度向量 我们需要得到最优的加权线性组合的参数 即矩阵 W 和偏移向量 b

    1. 因为 softmax 的输入是向量 因此把图片展开成向量 不过会损失很多空间信息 数据集有 10 个类别 则输出向量的维度就是 10
    2. 初始化参数 包括权重矩阵 W 和偏移向量 b
    3. 定义 softmax 函数 即对于一个向量做指数归一化
    4. 定义模型函数 即把一批次的输入向量展开成矩阵 比如一批次是 256 每一个输入向量有 784 个特征（图片有 28*28 像素） 那么矩阵就是 256*784 的 然后右乘 W 矩阵（784*10） 产生 256*10 的矩阵 在加上偏移向量 b（通过广播机制扩展成同维度的矩阵） 得到了最终的输出矩阵 即 256 个维度为 10 的置信度向量
    5. 实现交叉熵损失函数 需要用到花式索引
    6. 实现一个准确率函数 计算预测置信度和实际置信度一致的百分比
    7. 进行训练 使用梯度下降法进行迭代 最后使用测试集来测试准确率

常用损失函数

  • MSE：均方误差
  • L1：绝对值误差
  • Huber 鲁棒：分段采用均方和绝对值误差 使得损失函数一阶可微

CH10 感知机

单层感知机

  • 单层感知机模型是一种二分类模型 其求解算法等价于梯度下降法 有收敛定理 确保在有限次迭代后可以找到一个解
  • 单层感知机无法解决 XOR 问题 因为单层感知机只能产生一条分割线 而 XOR 需要两条分割线

多层感知机

  • 多类分类即在 softmax 回归的基础上加上隐藏层 这样就实现了非线性模型
  • 隐藏层数和隐藏层的神经单元数都是超参数 输入维数很高而输出维数很低时 可以通过多层隐藏层来慢慢的降维压缩信息
  • 通常会调高隐藏层数而不是隐藏层的神经单元数 这是因为隐藏层的神经单元数过多会导致过拟合
  • 隐藏层需要非线性的激活函数 否则多层感知机和线性模型等价

激活函数

  • ReLU：即 max(0,x)
  • Sigmoid：即 1/(1+exp(-x)) 投影到(0,1)之间
  • Tanh：即 (exp(x)-exp(-x))/(exp(x)+exp(-x)) 投影到(-1,1)之间

CH11 模型选择、欠拟合和过拟合

模型选择

  • 训练误差和泛化误差：训练误差是模型在训练集上的误差 泛化误差是模型在测试集上的误差 我们关心的是后者
  • 验证数据集和测试数据集：验证数据集用于评估模型超参数好坏并据此调参选模 测试数据集用于评估模型的泛化误差 两者绝对不能混用
  • K 折交叉验证：将数据集分成 K 份 每次取一份作为验证集 其余作为训练集 进行 K 次训练和验证 最后取平均值作为模型的泛化误差

过拟合和欠拟合

  • 欠拟合：模型无法得到较低的训练误差 通常是因为模型太简单
  • 过拟合：模型在训练集上表现很好但在测试集上表现很差 通常是因为模型太复杂
  • 模型容量：模型拟合各种函数的能力 容量越大 可以记住的数据特征越多 训练误差会随着模型容量的增加而减小 但泛化误差会先减小后增大
  • 估计模型容量：参数个数和参数值范围是两个重要的因素
  • VC 维：模型可以完美拟合任意数据集的最大容量 比如 2 维输入的线性模型的 VC 维是 3

CH12 权重衰退

  • 通过限制参数值的选择范围来降低模型的复杂度 从而减少过拟合 通常限制权重而不是偏移
  • L2 范数正则化：即在损失函数中加入权重的平方和的一半作为罚函数 通过调整超参数 λ 来调整正则化的强度 是一种柔性约束
  • 权重衰退通过 L2 范数正则化使得模型参数不会过大 从而控制模型的复杂度 减少过拟合

CH13 丢弃法

  • 动机：一个好的模型 对于多噪音的数据集应该是鲁棒的 在数据中加入随机噪音等价于 Tikhonov 正则化
  • 丢弃法对于每一个元素做如下扰动：以概率 p 丢弃该元素 以概率 1-p 保留该元素 从而保证期望不变 实现模型复杂度的控制 让模型更加抗干扰
  • 丢弃概率 p 是一个超参数
  • 通常将丢弃法作用于隐藏层的输出 即去掉某些神经元 只在训练时使用 在测试时不使用
  • 丢弃法有点像是丢弃神经元后的各个子神经网络的集成 不过现在更多认为是一种正则化方法
  • dropout 是现在比较主流的随机超参数调整方法

CH14 数值稳定性+模型初始化和激活函数

数值稳定性

  • 在深度模型中由于层数过多 可能会有多个数累乘的情况 这样会导致数值不稳定 从而导致梯度消失或爆炸

  • 梯度消失：梯度在反向传播过程中会不断的累乘 如果梯度小于 1 那么会不断的缩小 最后会消失

  • 梯度爆炸：梯度在反向传播过程中会不断的累乘 如果梯度大于 1 那么会不断的放大 最后会爆炸

模型初始化和激活函数

  • 思路：让每一层的输出方差尽可能相等 可以使得每一层的梯度尽可能相等 从而避免梯度消失或爆炸
  • 权重初始化：为了让每一层的输出方差尽可能相等 可以使用 Xavier 初始化方法 可以取均匀分布或正态分布
  • 激活函数：为了让每一层的期望和方差尽可能相等 激活函数必须近似于 f(x)=x 对于 relu 和 tanh 满足这个条件 而 sigmoid 则需要进行适当的线性变换
  • 总结：权重初始化和激活函数相当于对每一层的输出进行归一化 并不会丢失信息 让模型的数值稳定性更好 从而避免梯度消失或爆炸

CH15 Kaggle 比赛：房价预测

  • 先数据预处理：对于缺失值进行填充 对于类别特征进行 one-hot 编码 对于数值特征进行标准化
  • 选择模型：这里选择了一个简单的单层线性回归模型
  • K 折交叉验证：这里选择了 5 折交叉验证
  • 调整超参数：不断改变超参数 选出交叉验证平均误差最小的超参数

CH16 神经网络基础

  • Pytorch 中的 nn.Module 类是一个可供继承的类 代表一个神经网络模型 通过继承这个类可以实现自定义的神经网络模型
  • 访问state_dict属性可以得到模型的参数
  • Module 也可以用于自定义一个层
  • torch.load和torch.save可以用于保存和加载模型到文件

CH19 卷积层

  • 对于图像来说 全连接网络会导致参数过多 比如 100x100 3 通道的图像 有 30000 个参数 全连接层的参数会达到 30000x30000 个 因此需要卷积神经网络

  • 图片对象的识别有两个特点：平移不变性和局部相关性 即图片的特征不会因为平移而改变 而且图片的特征只和局部有关

  • 为了提取局部特征 我们采用卷积核 卷积核是一个权重矩阵 通过卷积核和图像的卷积来提取特征 卷积核矩阵会和图像的一个区域做按位相乘 然后做累加得到一个值 这个值作为这个区域的特征 比如边缘特征的矩阵是

    1
    2
    3
    -1 -1 -1
    -1  8 -1
    -1 -1 -1

    这是因为如果一个区域是边缘 这个累加就非 0 如果一个区域的颜色基本一致 这个累加就接近 0 这样就把边缘特征提取出来了

  • 卷积核的尺寸可以是矩阵 一般为奇数 保证有一个中心点

  • 对图像做卷积会导致图像的尺寸变小 因此需要 padding 来保持图像的尺寸 通常是在图像的外围填充一堆 0 保证卷积后的图像尺寸不变

  • 卷积核的深度和图像的深度是一样的 比如 3 通道的图像就需要 3 个卷积核

  • 池化：把一个区域的值映射到一个值上 比如最大池化就是把一个区域的最大值作为这个区域的值 目的是降低图像的尺寸 从而减少权重参数

  • 如何训练？

    • 卷积核矩阵的每一个数字都是一个参数

  • 通俗理解 卷积网络负责把一个大图像提取特征为小图像 再把小图像输入到全连接神经网络里进行分类 从而大大减少权重参数 其中卷积层就是对图像做特征提取 池化层就是对特征图像做模糊处理

CH20 卷积层的填充和步幅

  • 填充：即 padding 为了保持图像的尺寸不变 通常在图像的外围填充一堆 0 当图像尺寸较小 且希望使用较深的卷积核时 可以使用填充
  • 步幅：即 stride 为了减少图像的尺寸 通常在卷积的过程中每次移动的距离是 1 但是可以调整步幅来减少图像的尺寸 当图像较大 且因为计算资源限制需要减少图像尺寸时 可以使用步幅

CH21 多输入通道和多输出通道

  • 多输入通道：即输入的图像有多个通道 比如 RGB 图像就有 3 个通道 那么卷积核就是 3x3x3 卷积得到一个输出值（相当于 3 个二维卷积结果相加）
  • 多输出通道：即对于一个输入通道 有多个卷积核 每个卷积核都和输入图像做卷积 得到多个输出值
  • 意义：一个卷积核可以视为提取一个特征 通过加权组合 可以识别出多个特征的组合
  • 1 *1 卷积核：相当于对输入的不同通道进行重新组合 从而得到一个新的通道 等价于一个权重参数一样的全连接层 因此 1x1 的卷积核经常被用于改变通道数

CH22 池化层

  • 卷积对位置敏感 如果需要增强模型的平移不变性 我们需要池化层
  • 池化和卷积类似 只是池化的操作不一定是卷积的求和 比如最大池化就是取一个区域的最大值作为这个区域的值 平均池化就是取一个区域的平均值作为这个区域的值
  • 池化层的超参数与卷积层也类似 有 padding 和 stride 区别是池化层没有学习参数 因为池化层的操作是固定的
  • 池化层的通道是不可以融合的 因此池化层的输出通道数和输入通道数相等
  • 个人理解：卷积层除了提取出图像特征 还会提取出这个特征的位置信息 适用于对位置敏感的任务 而池化层只提取出是否存在这个特征 举个例子 一个模型的任务是识别图片中存不存在哈基米 那么如果哈基米出现在不同位置 卷积层会识别为不同的特征 而池化层会识别为同一个特征
  • 通常将池化层连接在卷积层之后 以缓解卷积层对于位置的敏感性

CH23 LeNet

  • LeNet 是 80 年代末期由 Yann LeCun 提出的一个卷积神经网络模型 当时的目的是用于手写数字识别
  • LeNet 的结构是：输入层 -> 卷积层 -> 池化层 -> 卷积层 -> 池化层 -> 全连接层 -> 输出层
  • 总结一下 即使用了卷积层提取图片空间信息 然后使用全连接层来转换到类别空间

CH24 AlexNet

  • AlexNet 是一个深度卷积神经网络模型 由 Alex Krizhevsky 提出的 用于图像分类 赢得了 2012 年的 ImageNet 比赛
  • AN 可以视为更深的 LeNet 模型 其主要改进在于丢弃法、ReLU 激活函数、池化层与数据增强 另外新加了 3 层卷积层与更多的输出通道 最终参数量达到 LeNet 的 10x 计算量达到 LeNet 的 260x
  • AN 标志着深度神经网络的热潮开始

CH25 VGG

  • VGG 是一个深度卷积神经网络模型 由 Karen Simonyan 和 Andrew Zisserman 提出的 用于图像分类 赢得了 2014 年的 ImageNet 比赛
  • 作者发现卷积层深且窄的模型比卷积层浅且宽的模型效果更好 因此提出 VGG 块的结构 包括 n 层 m 通道的 3x3 卷积层和一个 2x2 池化层
  • VGG 就是多个 VGG 块后面接一个全连接层 比如 VGG-9 就是 9 个 VGG 块后面接一个全连接层
  • LeNet 是 2 个卷积层+1 个池化层+1 个全连接层 AlexNet 更大更深 并且使用了丢弃法和 ReLU 激活函数等新方案 VGG 则是更大更深的 AlexNet 其主要改进在于使用了更小的卷积核和更深的卷积层

CH26 NiN

  • 前面提到的几个 CNN 都用全连接层作为最后的分类器 但是全连接层的参数量太大了 可能出现过拟合的问题
  • NiN 块是一个卷积层后跟两个全连接层（也就是 1x1 卷积） 这样就可以减少参数量
  • NiN 架构就是多个 NiN 块和步幅为 2 的最大池化层交替组合 最后使用全局平均池化层和 softmax 分类器输出
  • NiN 块对每个像素增加了非线性性（本质上还是最后的 ReLU 增加的）全局平均池化层则使得 NiN 具有更少的参数 不容易过拟合
  • 池化层主要是降低模型复杂度 提高泛化性 但是相应的也会使得训练收敛速度变慢

CH27 GoogLeNet

  • GoogLeNet 是一个深度卷积神经网络模型 由 Christian Szegedy 提出的 用于图像分类 赢得了 2014 年的 ImageNet 比赛
  • 有趣的是 GoogLeNet 的名字是为了致敬 LeNet 然而其结构却和 LeNet 完全不同
  • Inception 模块是 GoogLeNet 的核心结构 其主要思想是通过 4 个不同的卷积路径抽取特征 然后在输出通道合并 其中 4 个路径分别为
    • 1x1 卷积
    • 3x3 卷积 1 padding
    • 5x5 卷积 2 padding
    • 3x3 最大池化层 1 padding
    • 每一条路径的通道数是不同的 比如 5x5 的通道数会少一点
  • 相比于单纯的卷积层 Inception 模块可以降低参数个数（主要是因为通过 1x1 卷积的降低了通道数）
  • GLN 比较像是谷歌用大量算力堆砌调参得到的一个模型 一般人应该不好模仿

CH28 批量归一化

  • 对于比较深的神经网络 损失出现在最后层 由于梯度反向传播会越来越小 会导致前面的层的参数更新比较慢 然而越往后的层提取的特征越高级抽象 这导致底层的参数一旦变化 上层的参数也需要跟着变（因为它们是在底层输出的基础上训练的）最终导致收敛速度变慢（因为必须得等底层稳定才能收敛整个模型）
  • 批量归一化希望底层参数更新时避免变化上层参数 如果每一层的输入都服从某一分布 即固定均值和方差 这会使得这一层参数更新的缓慢一些（因为不需要适应其他分布的数据）
  • 批量归一化层会作用在激活函数之前 使得数据都服从均值为 β 方差为 γ 的分布 这两个参数是可学习的
  • 批量归一化层作用在激活函数前 对于全连接层 作用在特征维 而对于卷积层 作用在通道维（也就是取出一个通道的所有图片的像素作归一化）
  • 后续研究指出 BN 可能是通过在每个 batch 中添加噪声来控制模型复杂度（存疑）
  • BN 可以加速收敛速度 但是一般不提高模型的精度 一般用于比较深的模型中

CH29 残差网络

  • 残差网络是一个深度卷积神经网络模型 由 Kaiming He 提出的 用于图像分类 赢得了 2015 年的 ImageNet 比赛
  • 深度网络的层数变多 不一定意味着模型的性能会变好 这是因为更深的网络的函数空间可能不能完全包含浅层网络的函数空间 ResNet 希望保证深度网络的函数空间包含浅层网络的函数空间 使得更深的模型的性能一定大于等于浅层模型
  • RN 的方法是残差块 也就是将一层的输出从 f(x)变为 f(x)+x 即将输入连接到输出上
  • 可以理解为电路的短路 即残差块最差也只是 f(x)啥也没学到 输出就等于输入 这使得每一层网络一定不会降低整个网络的性能
  • 具体设计中 输入 x 会先经过一个 1x1 卷积层来组合通道 然后接到输出上
  • ResNet 块包含两种 一个是高宽减半的块 另一个是高宽不变的块 总体架构和 VGG、GoogLeNet 类似

CH30 第二次竞赛-图像分类

CH31 CPU 和 GPU

CH32 TPU 和其它

CH33 单机多卡训练

CH34 多 GPU 训练

CH35 分布式训练

论文研读

AlexNet

  • 2012 年 ImageNet 比赛的冠军
  • 背景
    • ImageNet 是一个大规模的图像数据集 包含了 1000 个类别的 120 万张图像
    • 之前的模型都是使用传统的机器学习方法进行特征提取 然后使用 SVM 等分类器进行分类
    • AlexNet 是第一个使用深度卷积神经网络进行图像分类的模型
  • 意义
    • AlexNet 的成功证明了深度学习在计算机视觉领域的有效性
    • AlexNet 的成功也推动了深度学习在其他领域的应用

ResNet

  • 2015 年 ImageNet 比赛的冠军
  • 背景
    • 随着深度学习的发展 模型的深度越来越深 但是深度过深会导致梯度消失或爆炸的问题
    • ResNet 提出了残差学习的概念 通过引入跳跃连接来解决深度网络训练中的梯度消失和爆炸问题
    • 可以简单理解为 以前训练的是 f(x) 现在训练的是 f(x)+x 这样就可以避免梯度消失和爆炸的问题
  • 意义
    • ResNet 的成功证明了深度网络可以训练得更深
    • ResNet 的成功也推动了深度学习在其他领域的应用

Transformer

  • 2017 年提出的 seq2seq 模型 使用了自注意力机制 没有依赖于卷积或循环神经网络 在翻译任务上取得了很好的效果 事到如今 已经在自然语言处理、计算机视觉等领域都有了广泛的应用

  • 在 TF 之前 主流的序列模型是 RNN 和 LSTM 它们的缺点是无法并行化 而自注意力机制可以并行化

  • CNN 对于长序列的建模能力有限 这是因为 CNN 的感受野有限 距离比较大的信息需要多层卷积才能传递到一起 而自注意力机制可以直接建模任意两个位置之间的关系 另外多头注意力机制模仿的是 CNN 的多输出通道 用于提取不同的特征

  • En-De 架构就是把序列变为等长的向量 然后再变为一个不一定等长的序列 解码器和编码器不一样的地方在于其是自回归的 即每次只预测一个词 不像编码器是一次性理解整个序列

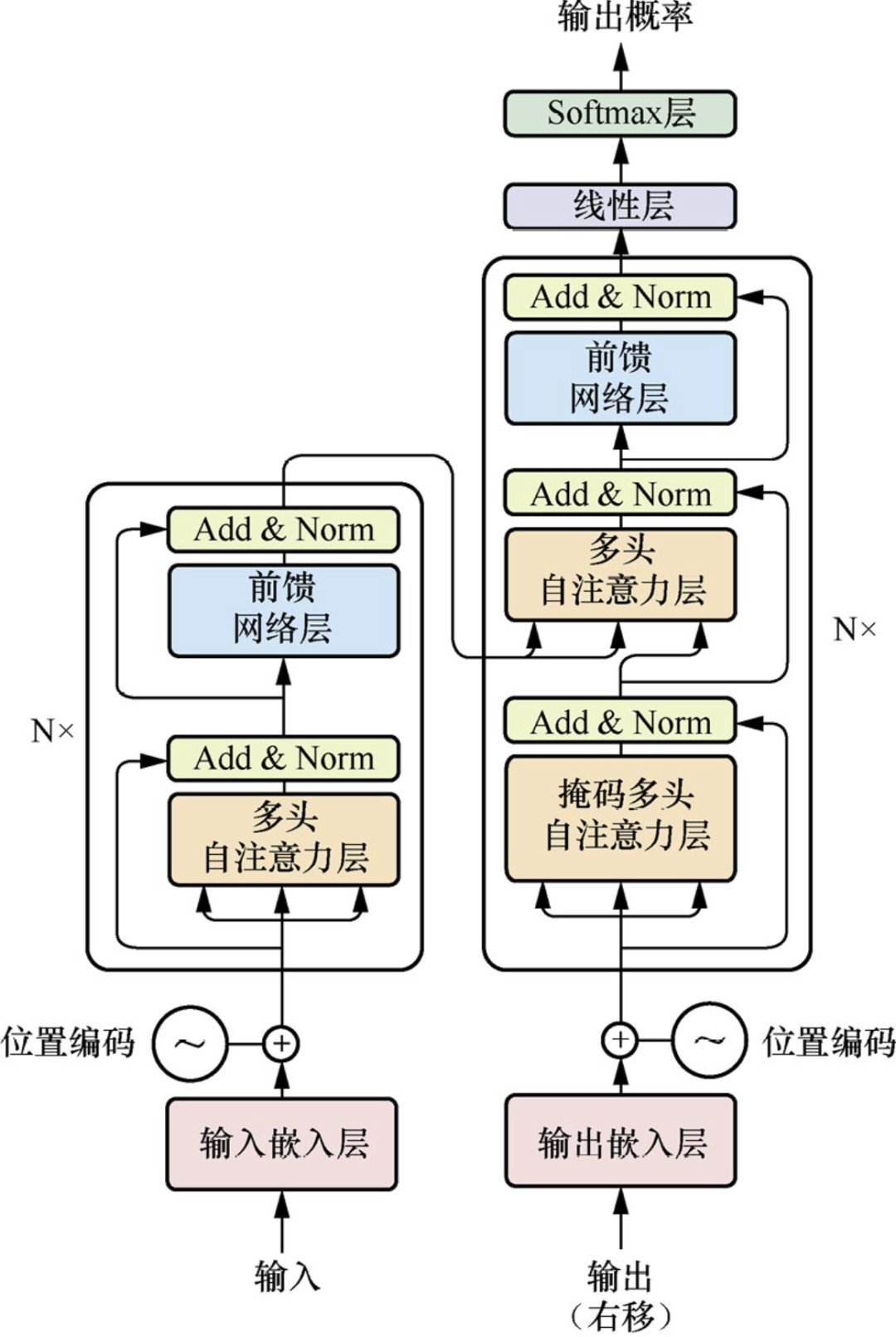
  • 模型结构：alt-text

    • 整个模型包括编码器、解码器、输入嵌入、输出嵌入以及最后的一个线性 softmax 层
    • 编码器的架构很简单 有 N 个块 每个块中包含两个子层：多头自注意力层和前馈神经网络层 其中每个子层都有一个残差连接和层归一化 整个编码器的超参数只有 2 个 N 和 d_model 前者是块数 后者是每个块输入输出的维度（为了方便残差处理 输入和输出的维度是一样的）
      • 每个子层的最终输出可以认为是 LN(x+Sublayer(x))
      • Embedding：即将每个单词嵌入为一个向量
      • Positional Encoding：为了保留序列的顺序信息 我们需要对每个单词的向量加上一个位置编码 这个位置编码是一个正弦函数和余弦函数的组合 这样可以保证每个单词的向量都是唯一的 这个位置编码和嵌入相加之后输入到多头自注意力层
      • LayerNorm：BatchNorm 就是把一个 batch 的数据中的一个列进行归一化 而 LayerNorm 是把一个 batch 的数据中的每一行进行归一化 对于序列数据而言 前者是取出了一个特征上整个 batch 和 seq 的数据 而后者是取出了一个样本的整个 seq 和所有特征的数据 如果序列数据的长度差别较大 BN 每次算出的均值和方差往往差别也较大 使得模型不稳定 泛化性差 而 LN 是对每个样本计算均值和方差 相对稳定、
      • Self-Attention 机制
        • 具体步骤
          1. 将每个单词 embedding 为一个向量 H
          2. 通过三个矩阵 Wq、Wk、Wv 将每个单词的向量映射为三个向量 Q、K、V
          3. 计算每个单词组合的 Q 和 K 的点积 最终得到一个权重矩阵 A 代表了单词 i 与单词 j 的相关性 也即注意力权重
          4. 用 softmax 函数将权重矩阵归一化
          5. Hi’ = ∑(Aij * Vj) 其中 Aij 是单词 i 对于单词 j 的注意力 Vj 是单词 j 的向量 这个 Hi’ 就是单词 i 的新的理解
        • 计算过程类似于矩阵运算 因此显然可以并行化 具体而言
          1. Q = H * Wq, K = H * Wk, V = H * Wv
          2. A = softmax(Q * K^T / sqrt(dk)) 其中 dk 是 K 的维度 是一个正则化项 防止点积过大
          3. H’ = A * V
      • Multi-Head Attention：即将 Q、K、V 分成 h 组 然后分别计算每一组的注意力权重 最后将所有的注意力权重拼接起来 这样可以提取出不同的特征
      • Feed-Forward Network：即对每个单词的向量做 MLP 这个和 RNN 的做法是类似的 RNN 中 MLP 的输入是上一个输出和当前输入 而这里 MLP 的输入就是经过注意力计算后的向量 都是对于已经做语义嵌入后的向量进行处理
      • 我的理解：多头注意力层输入一个序列（嵌入） 这个嵌入代表对于每一个词的特征的理解 经过多头注意力层后 输出的还是一个嵌入 代表的还是对于每一个词的特征的理解 但是这个理解是基于自注意力机制的计算后 更加完善的理解 其特征更加的丰富和准确 至于 Q、K、V Q 和 K 分别代表单词 i 和 j 做点积就是计算单词 i 和 j 的相关性 V 代表需要取出单词 j
    • 解码器的架构和编码器类似 只是多了一个子层：掩码多头自注意力层
      • 掩码多头自注意力层：在计算注意力权重时 只考虑当前单词和之前的单词 这样就可以保证解码器是自回归的 具体实现中 会将 t 之后的注意力权重置为-inf
      • 第一个掩码层输出的 Q 与编码器输出的 K、V 作为第二个子层的输入 这里可以理解为模型先理解当前已生成的序列 得到查询 Q 然后去输入序列中寻找相关的上下文信息 K、V 用于生成下一个单词
      • 我的理解：第一个掩码层代表解码器对于已有输出序列的理解 第二个注意力层输入的代表了已有序列和输入序列 用注意力去查询重要的部分 输出最终的理解

GNN/GCN

GNN

  • GNN（Graph Neural Network）即图神经网络 是一种用于处理图数据的深度学习模型
  • GNN 中 节点的特征表示为一个向量 边同理 除此之外还有一个全局 U 的表示
  • 针对图数据 主要有 3 种任务
    • 图层级任务：如对整个图进行分类
    • 节点层级任务：如对每个节点进行分类
    • 边层级任务：如预测边的特征
  • 图数据一般预处理成如下的形式
    • Nodes：节点的特征向量数组
    • Edges：边的特征向量数组
    • Adjacency List：邻接表 代表第 i 条边的起点和终点
    • Global：全局的特征向量
    • 比如：
      1
      2
      3
      4
      Nodes = [[1,2],[3,4],[5,6]]
      Edges = [[0,1],[1,2],[2,0]]
      Adjacency List = [[1,2],[0,2],[0,1]]
      Global = [7,8]
  • GNN 输入一个图 G 输出一个变换后的图 G’ G’的特征可能会改变 但是连通性不变
  • GNN 的基本结构
    • 输入：图 G 的节点特征矩阵 Vn、边特征矩阵 En、全局特征矩阵 Un
    • 对应三者有三个 MLP 每个 MLP 输入的是特征向量而非整个矩阵 组成了 GNN 的一个层 由于不对 Adjacency List 进行处理 因此图的连通性不变
    • 输出：图 G’的节点特征矩阵 Vn+1、边特征矩阵 En+1、全局特征矩阵 Un+1
  • 如果缺少特征 可以通过汇聚操作
    • 汇聚操作是将邻居节点的特征向量进行加权平均或拼接等操作 然后加上全局特征向量
    • 比如缺少顶点特征 可以汇聚邻居节点的特征 或是汇聚邻边特征

GCN

  • 可以看到 目前的 GNN 没有使用任何的结构信息 因此需要信息传递
    • 信息传递和汇聚类似 即把邻居节点的特征汇聚到当前节点上再输入 MLP
    • 对于图来说 这样的信息传递相当于权重相同的卷积操作
    • 更复杂的传递还可以包括边到节点的传递 只需要用矩阵投影到相同的维度即可
    • 比如先点后边的传递：
      1. 节点先将邻接边的特征进行汇聚 更新特征向量
      2. 边再将起点和终点的特征进行汇聚 更新特征向量
    • 其中点边顺序的不同是有影响的 没有证明说哪种顺序更好 甚至可以交替进行
  • 全局特征 U
    • 如果一个图过于稀疏 信息传递往往比较慢
    • 作者设计了一个虚拟的全局节点 U 这个节点和所有节点与所有边都有连接 因此在信息传递时每个特征向量都会和 U 进行信息传递 同时 U 也会汇聚所有节点和边的特征
    • 个人理解 U 相当于全局特征提取 用于加速收敛

GAN

  • GAN（Generative Adversarial Network）即生成对抗网络 是一种用于生成数据的深度学习模型
  • GAN 的基本思想是通过两个神经网络进行对抗训练 一个生成器 G 和一个判别器 D
  • 基本结构
    • 假设数据 x 的真实分布是 p_g 我们通过生成器 G 来拟合这个分布 也即 G(z;θg) 其中 z 是一个符合 p_z 分布的噪声向量（维度可以和输出不一样）θg 是 G 的参数
    • 判别器 D(x;θd) 用于判断输入的 x 是真实数据还是生成数据 其中 θd 是 D 的参数 输出的值是一个概率值 0-1 之间
    • G 的损失函数是 log(1-D(G(z))) 即希望骗过 D
    • D 的损失函数是 log(D(x))+log(1-D(G(z))) 即希望正确判断真实数据和生成数据
    • 因此最终的损失函数为
      1
      min_G max_D V(D,G) = E_x~p_g[log(D(x))] + E_z~p_z[log(1-D(G(z)))]
      这个损失函数是一个对抗性损失函数 最终会达到一个纳什均衡 即 D 和 G 都无法再继续优化损失函数
    • 具体流程
      1. 从真实分布中采样数据 x 从噪声分布中采样数据 z
      2. 输入数据到判别器 D 中 计算损失函数
      3. 根据损失函数更新判别器 D 的参数
      4. 循环 1-3 步 k 次
      5. 从噪声分布中采样数据 z
      6. 输入数据到生成器 G 中 计算损失函数
      7. 根据损失函数更新生成器 G 的参数
      8. 循环 1-7 步 直到收敛
    • 可以看到超参数 k 会影响对抗训练的有效性 k 过大会使得 D 更新过快 导致损失函数接近于 0 使得梯度消失 k 过小则会使得 D 更新过慢 导致损失函数基本不变 使得 G 无法更新
    • GAN 的收敛判定是非常复杂的 后续的研究中提出了很多收敛判定的方法
    • 论文提出 在训练的初期 D 非常容易判断出真假数据 这导致前文提到的问题：损失函数接近于 0 导致梯度消失 论文提出可以把 G 的损失函数改为最大化 log(D(G(z))) 这样就可以避免梯度消失的问题 但是也带来了负无穷的数值问题
  • 论文通过数学证明了：当且仅当 D 和 G 都是最优时 损失函数取到最小值 即损失函数是可以成功训练 D 和 G 的

BERT

  • BERT（Bidirectional Encoder Representations from Transformers）是由 Google 提出的预训练语言模型 使用了双向的 TF 用于自然语言处理任务
  • 在 BERT 之前 主流的预训练语言模型是 ELMo 和 GPT
    • ELMo 是一个双向的语言模型 但是是基于 RNN 的
    • GPT 是一个单向的语言模型 是基于 TF 的
    • BERT 是一个双向的语言模型 是基于 TF 的 结合了两者的优点
  • BERT 模型有两个步骤
    • 预训练：使用大规模的无标签文本数据进行预训练 主要是为了学习语言的表示
    • 微调：用预训练的结果初始化权重参数 然后再使用小规模的有标签文本数据进行微调 从而训练出一个下游任务的模型
  • BERT 的预训练任务有两个
    • Masked Language Model：随机掩码输入序列中的一些单词（即用 mask 替换）然后训练模型去预测这些单词
    • Next Sentence Prediction：预测两个句子是否相邻 即预测语句 B 在语句 A 后面的概率
  • 基本架构
    • BERT 输入的文本是一个句子对 其中第一个句子是 A 第二个句子是 B 然后用一个特殊的分隔符 [SEP] 将两个句子分开 在句子 A 的开头加上一个特殊的开始符号 [CLS] 作为整个句子的表示
    • 输入的 token 需要进行嵌入 这个嵌入是一个向量 这个向量是由三个部分组成的
      • Token Embedding：即将每个单词嵌入为一个向量
      • Segment Embedding：即将每个句子嵌入为一个向量 用于区分句子 A 和句子 B
      • Position Embedding：即将每个单词的位置嵌入为一个向量 用于保留序列的顺序信息
    • MLM 需要对输入的文本进行掩码处理 随机选择 15%的单词进行掩码 然后将掩码的单词替换为 [MASK] 其他的单词不变 为了和微调时的输入保持一致 需要做以下处理
      • 80% 的概率替换为 [MASK]
      • 10% 的概率替换为随机的单词
      • 10% 的概率不变（但是要用于预测）
    • NSP 输入的文本是一个句子对 A 和 B B 有 50%的概率是 A 的下一个句子 50%的概率是随机的句子

ViT

  • ViT（Vision Transformer）是 由 Google 于 2020 年提出的一个图像分类模型 使用了 TF 的架构 将图片视为多个 patch 输入给 TF 进行训练
  • ViT 将输入的图片划分为 16x16 的 patch 一个 patch 相当于一个 word 一张图片相当于一个语句序列 一个 patch 展平后投影得到的向量相当于一个 word embedding 位置编码类似于 NLP 是 patch 在图片中的位置
  • 模型架构
    • 假如输入的图片是一个 224x224 的 RGB 图片 将其划分为 16x16 的 patch 得到 196 个 patch 每个 patch 展平后投影得到的向量是一个 768 维的向量（因为 3 个通道）
    • patch 向量先经过一个 768x768 的矩阵 被称为线性投影层 将每个 patch 的向量投影到一个 768 维的空间中 这个矩阵是可学习的 输出的向量称为 patch embedding
    • 类似于 BERT ViT 在整个 patch 序列的开头加上一个特殊的向量 [CLS] 也是 768 维 这个向量在 TFE 中也会和其它所有向量互相作用 因此可以理解为这个向量是整个图片的表示 最终 CLS 向量用于分类
    • 位置编码相当于一个表格 记录了每一个位置的编码向量 也就是一个 197x768 的矩阵 将位置编码和 patch 的向量相加
    • 最终输入 TFE 的是 197 个 768 维的向量 其中第一个是 [CLS] 向量 后面 196 个是 patch 向量 一个 Encoder 可以包含多个多头注意力块
  • 消融实验
    • 论文提到 ViT 也可以将输出的 patch embedding 输入一个全局平均池化层 然后进行分类 其效果和 CLS 向量的效果差不多（但是需要的学习率不一样） 但是为了保持原有的 TF 架构 论文采用了后者 从而证明 TF 原生的架构就可以高效处理 CV 任务
    • 论文提到 位置编码可以采用 1-D 的（1 2 3…） 也可以采用 2-D 的（1,1 1,2 1,3…） 也就是说 1-D 的是 196 个 768 维的向量 而 2-D 是 14+14 个 384 维的向量代表第 i 行和第 j 列的位置编码 然后只需要将两个向量拼接成 768 维的向量即可 最终实验证明位置编码的格式无所谓 因此还是采用了和 TF 一样的 1-D 编码
  • 归纳偏置
    • CNN 包括主要的 2 个归纳偏置：局部性和平移等变性
    • TF 却没有这些归纳偏置 是全局理解序列的 因此论文认为小数据集上不如 CNN 是正常的 在大数据集下两者性能可以媲美
    • 论文也提到混合 CNN 和 TF 的模型 也就是用 CNN 来处理 patch 得到 embedding 在小数据集上表现较好

MAE

  • MAE（Masked Autoencoder）是 由 Facebook 于 2021 年提出的一个图像分类模型 使用了 TF 的架构 将图片视为多个 patch 输入给 TF 进行训练 类似于 BERT 结合了 ViT 从而可以用于图片任务
  • 基本架构
    • 输入的图片仍被划分为多个 patch 其中有 75% 的 patch 被掩码掉 25% 的 patch 被保留
    • 保留的 patch 输入 encoder（一个 ViT） 得到相同维度的向量 其中额外包含一个 mask token 这个 mask token 是一个可学习的参数 用于代表掩码掉的 patch 的特征向量
    • 所有特征向量经过一个 decoder（一个 MLP）生成图片的 patch 和原始图片计算损失
    • 微调时 只需要使用 encoder 输出的特征向量 后接自己的网络即可
人工智能
#深度学习 #机器学习
从零开始深度学习
https://nwdnys1.github.io/2024/09/21/深度学习/
作者
nwdnysl
发布于
2024年9月21日
许可协议